Выбор основных характеристик промыслового судна (Аполлинариев В.И.) (УДК 629.124.72.001.57)

Строительная стоимость крупного промыслового судна измеряется десятками миллионов рублей, годовые эксплуатационные затраты и прибыль - миллионами, число однотипных судов - десятками. Поскольку оптимизация улучшает показатели на 5-10 %, с 60-х гг. постоянно ведутся работы по применению методов оптимизации в проектировании и эксплуатации промысловых судов. Особую роль приобретают эти методы в условиях перехода к рыночной экономике.

Оптимизация характеристик промыслового судна осложняется наличием случайных факторов в его эксплуатации и неопределенностью, связанной с долгосрочным прогнозированием.

Для оптимизации основных характеристик траулера-завода разработана специализированная имитационная модель, представляющая собой комплекс программ из двух блоков для ЭВМ. Первый в соответствии с входными данными вычисляет технические параметры судна. Второй блок имитирует процесс эксплуатации в случайно меняющихся условиях, подсчитывает технико-экономические показатели. Модель дает возможность экспериментально оценивать эксплуатационные характеристики судна на самых ранних стадиях его проектирования.

На условном примере рассмотрим применение имитационной модели для выбора основных характеристик траулера-завода в условиях неопределенной продуктивности сырьевой базы.

Положим, требуется спроектировать крупнотоннажный траулер-морозильщик для следующих условий:

объект лова - ставрида; выпускаемая продукция - мороженая обезглавленная потрошеная рыба, рыбная мука из отходов и непищевого прилова; доля пригодной к обработке рыбы - 80 %; удаленность района промысла - 5000 миль; цены, нормативы и организация промысла соответствуют Западному бассейну; продуктивность сырьевой базы характеризуется средними уловами некоторых типов судов за сутки лова (табл. 1).

В имитационной модели улов за траление - случайная величина, закон распределения которой зависит от пяти параметров. Четыре из них вычисляются в функции математического ожидания. Последнее считается по формуле

где u - математическое ожидание улова за траление, т; γ - коэффициент продуктивности сырьевой базы; N - располагаемая мощность на винте в режиме траления, кВт.

Коэффициент γ определяется следующим образом. Для судов, уловы которых известны, экспериментально на имитационной модели строятся зависимости средних уловов за сутки лова от γ (рис. 1). С этих графиков снимаются значения γ для каждого судна и осредняются в соответствии с объемом выборки (см. табл. 1).

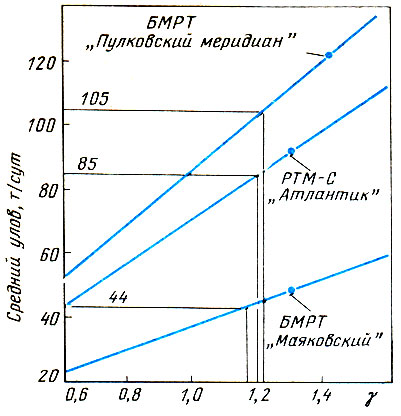
Рис. 1. Зависимость среднего улова за сутки промысла от коэффициента продуктивности сырьевой базы

Пусть по прогнозу сырьевая база для проектируемого судна остается ±10%.

Таблица 1

Сначала проведем оптимизацию без учета неопределенности, т. е. полагая γ=1,2. Параметры и результаты оптимизации приведены в табл. 2. В качестве критерия оптимизации приняты относительные приведенные затраты. Оптимизация проводилась методом наискорейшего спуска. Начальные значения оптимизируемых параметров примерно соответствуют БМРТ типа "Пулковский меридиан".

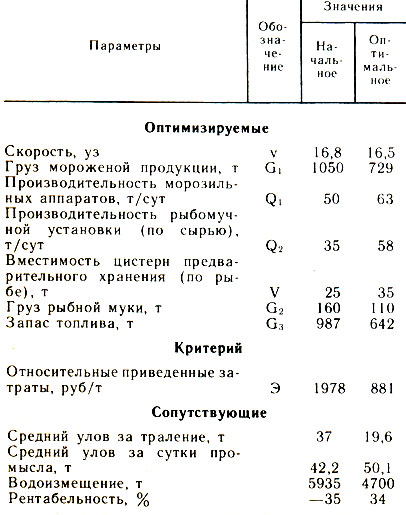
Таблица 2

Для уточнения точки оптимума и оценки влияния продуктивности сырьевой базы на результат оптимизации проводится квадратичный эксперимент.

Получим зависимость оптимизируемых параметров от изменения коэффициента сырьевой базы:

v = 16,5-0,003δ;

G₁ = 755-15,8δ;

Q₁ = 67-0,34δ;

Q₂ = 63,4-0,037δ-0,0014δ²;

V = 36-0,22δ;

G₂ = 118-50,5δ+0,054δ²;

G₃ = 649-15,5δ+0,041δ²,

где δ - относительное изменение коэффициента сырьевой базы:

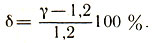
Получим выражение для относительных приведенных затрат

Для иллюстрации влияния сырьевой базы в табл. 3 приведены значения оптимизируемых параметров и критерия для некоторых значений δ, из которых ясно, что с увеличением продуктивности сырьевой базы оптимальные параметры судна в целом заметно уменьшаются. Производительность обрабатывающего комплекса уменьшается незначительно, на фоне уменьшения судна ее можно считать возрастающей.

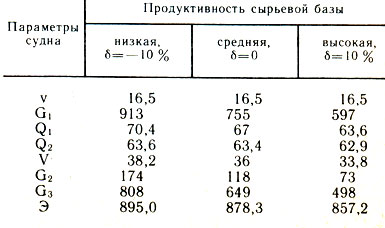
Таблица 3

Проделанные выкладки и полученные результаты относятся к случаю, когда прогноз сырьевой базы точен. Оценим последствия неточного определения продуктивности сырьевой базы. Пусть параметры судна определялись в предположении, что отклонение сырьевой базы будет равно δ, а его реальное значение оказалось Δ. В этом случае относительные приведенные затраты будут равны

Для наглядности зависимость ΔЭ=Э(Х(δ),Δ)-878,3 представлена на рис. 2 в виде графиков.

Слагаемое 0,072 (δ-Δ)² естественно рассматривать как цену ошибки прогноза. Так, если ошибка (δ-Δ)² составит 5 %, то приведенные затраты на каждую тонну продукции возрастут на 1,8 руб.; при 10 % - 7,2 руб.; при 20 % - 28,8 руб. (Появляется возможность оценить целесообразные затраты на повышение точности прогноза.)

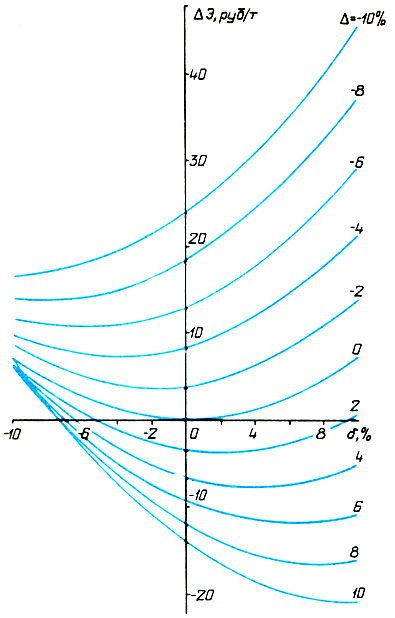
Рис. 2. Зависимость относительных приведенных затрат от ошибки прогноза

Вернемся к вопросу выбора параметров судна. Анализ данных рис. 2 показывает следующее. Если проектирование вести в предположении δ=-10%, относительные приведенные затраты будут иметь наименьший разброс значений (884,5≤Э≤895,0 руб/т). Такой подход приведет не к самым высоким, но надежным результатам (в теории игр такой подход называется стратегия "осторожного игрока"). Интересно отметить, что это соответствует увеличению размеров судна (см. табл. 3). (Не этот ли фактор в сочетании с обеднением сырьевой базы привел к укрупнению промысловых судов?)

Существует и другой подход (стратегия "азартного игрока"), который заключается в следующем. Величина Δ рассматривается как случайная. Величина δ выбирается из условия минимума математического ожидания относительно приведенных затрат. Пусть математическое ожидание MΔ=v и дисперсия DΔ=σ². Тогда математическое ожидание относительных приведенных затрат равно

Очевидно, минимум достигается при δ=v. Так, в нашем случае, если считать v = 0, при проектировании надо ориентироваться на δ=0 (см. табл. 3). В среднем (если прогноз является несмещенной оценкой) относительные приведенные затраты уменьшатся на 7,2 руб/т по сравнению с первым подходом. Но и риск в этом случае больше, так как интервал значений критерия шире (864,4≤Э≤902,2 руб/т), т. е. в худшем случае можно проиграть 7,2 руб/т.

Для корректного сравнения этих двух подходов необходимо знать статистические свойства прогноза (величину σ, наличие смещения, вид закона распределения). К сожалению, организации, занимающиеся прогнозом сырьевой базы, не публикуют (или не имеют) подобных данных. Более того, выбор того или иного подхода должен быть согласован с экономическим положением покупателя судна. Неопределенность в любом случае приводит к риску, степень его оправданности можно оценить изложенным методом с помощью экспериментирования на имитационной модели.

В рассмотренном примере степень неопределенности приводит к увеличению объема вычислений. Полученные результаты, разумеется, нельзя автоматически переносить на другие типы судов и иные ситуации, они соответствуют лишь тем условиям, в которых были получены.